Geometrija zapravo počinje razumijevanjem osnovnih oblika. Jedan od njih, pravokutni trokut, ima posebno mjesto.
Svaka stranica i kut u pravokutnom trokutu imaju precizno određen odnos. To se stalno pojavljuje, od građevine i inženjerstva pa sve do sasvim običnih situacija u svakodnevici.
Pravokutni trokut ima jedan pravi kut, dvije kraće stranice koje zovemo katete i najdužu stranicu nasuprot pravom kutu, poznatu kao hipotenuzu. Odnosi među njima temelj su Pitagorinog poučka i trigonometrijskih omjera.
Ako razumijete te odnose, možete prilično točno izračunati udaljenosti, visine ili kutove u stvarnom svijetu. Zvuči jednostavno, ali zapravo je nevjerojatno korisno.
Osnovne karakteristike pravokutnog trokuta
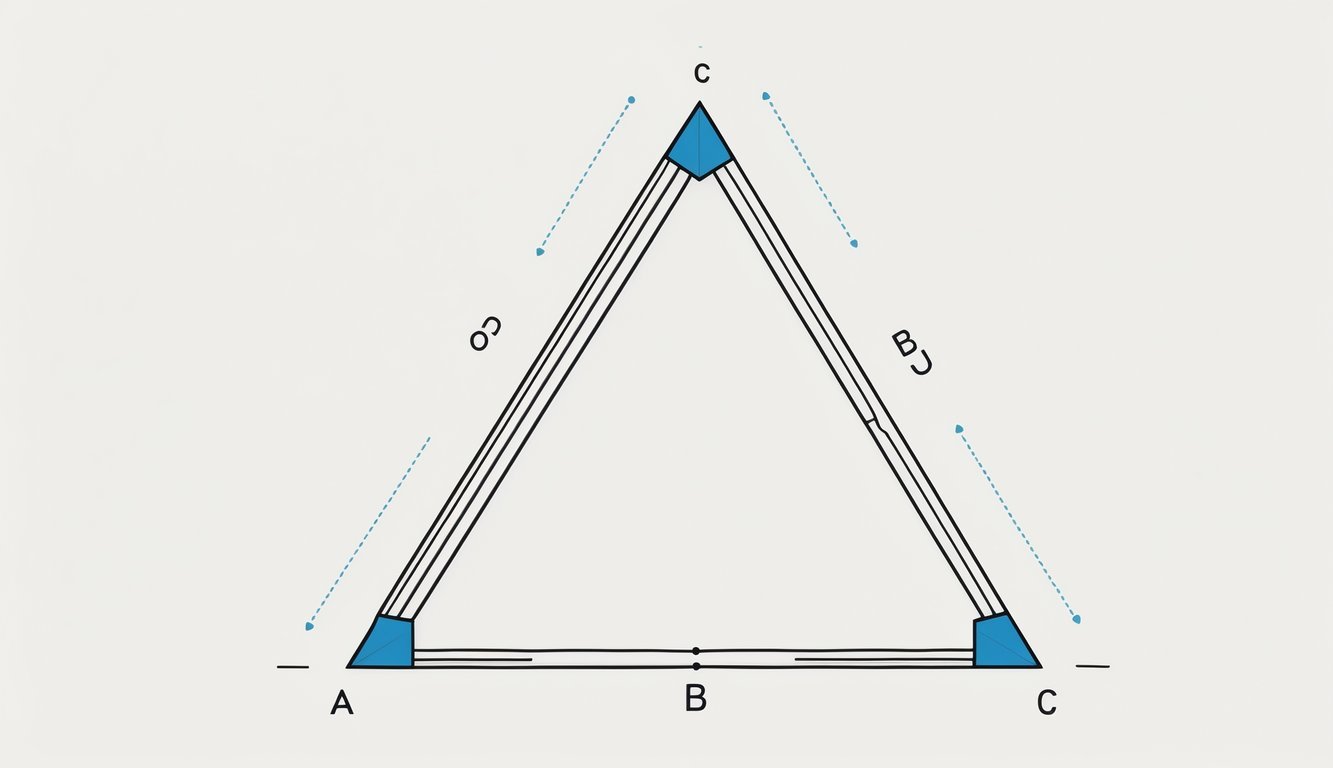
Pravokutni trokut temelji se na odnosima svojih stranica i kuteva. Ključni pojmovi su katete, hipotenuza i pravi kut.
Svaki od tih pojmova ima specifičnu ulogu u oblikovanju geometrijskih odnosa. Upravo ti odnosi čine osnovu trigonometrije.
Definicija i osnovni pojmovi
Pravokutni trokut je geometrijski lik s tri stranice i tri kuta. Jedan od tih kutova uvijek iznosi točno 90°.
Taj kut zovemo pravim kutom. Zbog njega trokut ima posebna svojstva.
Preostala dva kuta uvijek zajedno čine 90°, tako da ukupni zbroj kutova ostaje 180°. Nema iznimki.
U matematici se pravokutni trokut često koristi kao model za trigonometrijske funkcije — sinus, kosinus, tangens i kotangens. Te funkcije povezuju duljine stranica i kutove.
Zbog jednostavne strukture, pravokutni trokut olakšava rješavanje mnogih problema iz fizike, građevine i tehničkog crtanja. Njegove zakonitosti, poput Pitagorina poučka, čine ga nezaobilaznim u obrazovanju i svakodnevnim zadacima.
Stranice: katete i hipotenuza
Pravokutni trokut ima tri stranice koje se razlikuju po duljini i funkciji. Dvije kraće stranice su katete.
Katete zatvaraju pravi kut i čine osnovnu strukturu trokuta. One su međusobno okomite.
Ako pomnožite duljine kateta, dobit ćete površinu trokuta prema formuli:
[
P = frac{a times b}{2}
]
Treća stranica, hipotenuza, nalazi se nasuprot pravom kutu. Uvijek je najdulja stranica u trokutu.
Njezinu duljinu povezujemo s katetama Pitagorinim poučkom:
[
c^2 = a^2 + b^2
]
Ovaj odnos pomaže kad ne znate sve stranice napamet. U praksi, duljine kateta i hipotenuze koriste se kao polazište za mjerenja visina, udaljenosti ili kutova.
| Element trokuta | Položaj | Uloga |
|---|---|---|
| Kateta (a, b) | Uz pravi kut | Kraće stranice koje zatvaraju kut |
| Hipotenuza (c) | Nasuprot pravom kutu | Najdulja stranica, mjerilo odnosa stranica |
Pravi kut u pravokutnom trokutu
Pravi kut zapravo određuje identitet pravokutnog trokuta. Bez njega, trokut ne ulazi u ovu skupinu.
On dijeli trokut na dvije polovice koje su temelj za simetriju i razne konstrukcije. Pravi kut omogućuje definiranje odnosa između kateta i hipotenuze.
Zbog toga možemo koristiti trigonometrijske funkcije. Ako iznad kateta nacrtate kvadrate, površina kvadrata nad hipotenuzom jednaka je zbroju površina kvadrata nad katetama — to je Pitagorin poučak na djelu.
Pravi kut je ključan u određivanju visina i projekcija u prostoru. On daje trokutu stabilnost i zbog toga se često koristi u konstrukcijama ili mjerenju.
Matematički teoremi i formule
U pravokutnom trokutu odnosi između kateta i hipotenuze određuju posebne matematičke zakonitosti. Ti odnosi čine temelj za izračun duljina stranica, visina i kutova.
Pitagorin poučak
Pitagorin poučak opisuje vezu između stranica pravokutnog trokuta. Kaže da je kvadrat duljine hipotenuze jednak zbroju kvadrata duljina kateta.
[
c^2 = a^2 + b^2
]
Ova formula omogućuje izračun nepoznate stranice kad znate druge dvije. Na primjer, ako su katete 3 cm i 4 cm, hipotenuza će biti 5 cm.
Takve omjere zovemo pitagorejski trojci. U praksi, Pitagorin poučak koristi se u građevini, fizici, pa čak i u računalnoj grafici za određivanje udaljenosti između točaka.
Učitelji često pokazuju njegovu točnost pomoću kvadrata nad stranicama trokuta. Taj vizualni dokaz ostaje jedan od najprepoznatljivijih primjera geometrije.
Euklidov poučak
Euklidov poučak nadovezuje se na Pitagorin i bavi se visinom spuštenom na hipotenuzu. Kad povučete tu visinu, nastaju dva manja trokuta slična izvornom i jedan drugome.
Ta sličnost omogućuje izračun duljina pomoću odnosa segmenata hipotenuze. Euklid je definirao dva ključna odnosa:
- Kateta² = hipotenuza × projekcija te katete na hipotenuzu
- Visina² = dio1 × dio2 hipotenuze
Ovi odnosi omogućuju jednostavne izračune i bez trigonometrije. Često ih koristimo kad zadatak uključuje sličnost trokuta ili dokazivanje drugih tvrdnji.
Talesov teorem
Talesov teorem kaže da ako krajeve promjera kružnice spojite s bilo kojom točkom na kružnici, dobit ćete pravokutni trokut. Drugim riječima, trokut upisan u polukrug uvijek ima jedan kut od 90°.
Ovaj teorem spaja geometriju trokuta i kružnice. Primjena se jasno vidi kod konstrukcija opisane i upisane kružnice u pravokutnom trokutu, gdje hipotenuza čini promjer opisane kružnice.
Talesov teorem zapravo olakšava razumijevanje odnosa između pravaca i kružnica. U školi ga često koristimo za provjeru pravog kuta bez kutomjera, što je prilično praktično.
Izračuni u pravokutnom trokutu
Ako razumijete odnose između kateta i hipotenuze, možete izračunati opseg, površinu i visine trokuta. Matematičke veze koje ih povezuju temelje se na Pitagorinom poučku i trigonometriji.
To znanje olakšava rješavanje mnogih geometrijskih zadataka, bilo da ste u školi ili u stvarnom životu.
Izračun opsega i površine
Za pravokutni trokut, katete označavamo s a i b, a hipotenuzu s c. Pitagorin poučak vrijedi:
c² = a² + b².
Opseg trokuta računamo ovako:
O = a + b + c.
Najprije izračunamo hipotenuzu pomoću Pitagorinog poučka. Zbrojimo je s katetama i dobijemo opseg.
Površinu pravokutnog trokuta određujemo formulom:
P = (a × b) / 2.
Zapravo, ta formula proizlazi iz činjenice da pravokutni trokut čini polovicu pravokutnika sa stranicama a i b.
U tablici su prikazane osnovne ovisnosti:
| Veličina | Oznaka | Formula |
|---|---|---|
| Opseg | O | a + b + c |
| Površina | P | (a × b) / 2 |
| Hipotenuza | c | √(a² + b²) |
Visina na hipotenuzu i ostala svojstva
Visina spuštena iz vrha pravog kuta ima zanimljivo svojstvo. Dijeli pravokutni trokut na dva manja pravokutna trokuta, oba slična izvornom.
Ako visinu označimo s h, a dijelove hipotenuze s p i q, vrijedi:
h² = p × q.
Ova visina povezuje geometriju i algebru. Možemo izračunati sve stranice ako znamo dva podatka.
Središte opisane kružnice leži na polovištu hipotenuze. Polumjer je R = c/2.
Težišnica iz vrha pravog kuta jednaka je polovici hipotenuze (t = c/2). Takva pravilnost olakšava konstrukciju i provjeru točnosti na crtežu.
Podjela hipotenuze visinom
Kad povučemo visinu na hipotenuzu, ona je dijeli na dva segmenta, p i q. Ti dijelovi povezani su s katetama ovako:
a² = c × p i b² = c × q.
Drugim riječima, kvadrat duljine katete jednak je umnošku cijele hipotenuze i svog dijela.
Ova povezanost omogućuje da izrazimo sve stranice kroz međusobne odnose. Ne moramo koristiti trigonometrijske funkcije.
Kod praktičnih zadataka, ti odnosi pomažu brzo izračunati nepoznate duljine kad znamo samo stranice.
Sličnosti podtrokuta koji nastaju ovom podjelom često pomažu pri dokazivanju Pitagorinog poučka. U tehničkom crtanju to zna biti presudno za preciznost.
Trigonometrijski omjeri i primjena
Trigonometrija opisuje odnose između kutova i stranica pravokutnog trokuta. Pomaže nam izračunati nepoznate duljine i kutove u raznim situacijama, od gradilišta do navigacije.
Definicije: sine, kosinus i tangens
U pravokutnom trokutu svaka stranica ima određenu vezu s kutovima. Najduža stranica je hipotenuza, a preostale su katete — priležeća i nasuprotna.
Na temelju tih odnosa definiramo osnovne trigonometrijske omjere.
- Sinus (sin) kuta je omjer nasuprotne katete i hipotenuze.
- Kosinus (cos) je omjer priležeće katete i hipotenuze.
- Tangens (tan) označava omjer nasuprotne i priležeće katete.
| Omjer | Definicija | Formula |
|---|---|---|
| Sinus | nasuprotna / hipotenuza | sin α = a / c |
| Kosinus | priležeća / hipotenuza | cos α = b / c |
| Tangens | nasuprotna / priležeća | tan α = a / b |
Te tri funkcije su temelj trigonometrije. Njihove vrijednosti ovise samo o veličini kuta, ne o stvarnoj veličini trokuta.
Zato iste formule vrijede za svaki pravokutni trokut, bez obzira na veličinu.
Primjena trigonometrijskih omjera
Trigonometrijski omjeri koriste se u svakodnevnim i stručnim zadacima. Recimo, njima računamo nagib ceste, visinu zgrade ili duljinu ljestava potrebnu za dohvat određene točke.
Inženjeri ih koriste kod projektiranja mostova i krovova. Arhitekti njima određuju kutove između dijelova zgrade, a meteorolozi iz kuta elevacije računaju visinu oblaka.
U takvim zadacima najčešće znamo jedan kut i jednu stranicu. Pomoću odgovarajuće funkcije (sin, cos, tan) izračunamo nepoznatu duljinu.
Ovaj postupak je univerzalan i temelji se na jednostavnom omjeru stranica.
Rješavanje pravokutnog trokuta
Kad rješavamo pravokutni trokut, zapravo tražimo sve njegove kutove i stranice. U praksi postoje četiri osnovna slučaja:
- zadani su hipotenuza i kut,
- zadani su kateta i kut,
- zadane su hipotenuza i jedna kateta,
- zadane su dvije katete.
U svakom slučaju koristimo Pitagorin poučak i trigonometrijske omjere.
Ako znamo jedan kut i katetu uz taj kut, hipotenuzu računamo ovako:
c = b / cos α.
Kada znamo obje katete, do hipotenuze dolazimo Pitagorinim poučkom:
c² = a² + b².
Ovakav pristup daje precizan proračun bez kompliciranih alata. Zanimljivo je koliko često trigonometrija pravokutnog trokuta olakša život u tehničkim i znanstvenim zadacima.
Primjeri i zadaci iz svakodnevnog života
Razumijevanje trigonometrije i pravokutnog trokuta pomaže nam rješavati probleme u raznim tehničkim, prirodnim i svakodnevnim situacijama. Od mjerenja visine zgrade do projektiranja stepenica, odnosi među katetama, kutovima i hipotenuzom čine izračune bržima i sigurnijima.
Primjena u graditeljstvu i inženjerstvu
U graditeljstvu je pravokutni trokut gotovo svugdje. Arhitekti ga koriste za izračun kosina krovova, nagiba rampi i konstrukciju potpornih greda.
Kad projektiraju krov, primjerice, duljinu rogova računaju pomoću sinusnog i kosinusnog omjera iz poznate visine i širine. To štedi vrijeme i smanjuje potrebu za mjerenjem na terenu.
Inženjeri kod postavljanja mostova, antena ili električnih vodova također koriste osnovne trigonometrijske omjere. Ako znaju kut elevacije i vodoravnu udaljenost, visinu objekta ili duljinu kabela izračunaju pomoću formule
[ visina = udaljenost × tan(kut) ].
Takvi izračuni smanjuju pogreške na gradilištu i troškove ispravaka. Posebno kod planiranja nagiba cesta ili rješenja za odvodnju, trigonometrija pravokutnog trokuta daje potrebnu preciznost.
Rješavanje praktičnih zadataka
Ljudi svakodnevno, često bez razmišljanja, koriste principe pravokutnog trokuta. Na primjer, kad pokušavate izmjeriti visinu stabla pomoću njegove sjene.
Ili recimo, kad pokušavate otkriti udaljenost između dvije točke koje ne možete izravno mjeriti. Čak i kod uređenja doma, provjeravate jesu li zidovi poravnati.
Da biste riješili ovakve zadatke, obično radite kroz nekoliko koraka.
Prvo, prepoznajte što znate, a što ne znate.
Zatim nacrtajte skicu i označite kutove i stranice.
Nakon toga, koristite odgovarajuće trigonometrijske funkcije—sinus, kosinus ili tangens.
Na kraju, izračunajte i provjerite rezultat. Nije uvijek jednostavno, ali s vježbom ide lakše.
Evo jedan banalan primjer. Zamislite da je kut između tla i sunca 35°, a sjena zgrade duga 10 m.
Visinu zgrade dobijete tako da izračunate 10 × tan 35° ≈ 7 m.
Takvi zadaci baš lijepo povezuju matematiku s onim što zapravo radimo u životu.
Korištenje kalkulatora pravokutnog trokuta
Digitalni alati za trigonometriju stvarno olakšavaju svakodnevni rad. Kalkulator pravokutnog trokuta traži da uneseš dva poznata elementa — recimo, jednu katetu i kut — pa izračuna sve ostalo.
Možeš tako brzo doći do preostale katete, hipotenuze i kutova, bez puno muke. Tehničari, učenici i planeri terenskih radova često koriste ovakve alate.
Nema više ručnog računanja, što znači i manje šanse za grešku. Ali, treba barem okvirno razumjeti odnose među stranama trokuta.
Inače, lako se potkrade pogreška prilikom unosa podataka ili tumačenja rezultata. Evo kako izgleda tablica mogućih kombinacija podataka:
| Poznati elementi | Tražene vrijednosti | Koristi se funkcija |
|---|---|---|
| Kateta + Kut | Hipotenuza, 2. kateta | sin, cos |
| Hipotenuza + Kut | Obe katete | sin, cos |
| Katete | Kutovi, hipotenuza | tan, Pitagorin poučak |
Ako znaš ove odnose, kalkulator može biti stvarno koristan alat u nastavi i svakodnevnim izračunima.