Jeste li se ikada pitali kako dva pravca mogu stvoriti savršeni kut od 90 stupnjeva? U geometriji, taj odnos nije slučajan – to je čista matematika.
Okomiti pravci čine temelj za razumijevanje oblika, kutova i odnosa među linijama u ravnini. Nije to samo apstraktan pojam – u svakodnevici, arhitekturi i crtanju, okomiti pravci su osnova za svaki precizan prikaz.
Okomiti pravci su pravci koji se sijeku u jednoj točki pod pravim kutom, dijeleći ravninu na četiri jednaka dijela.
Bez okomitih pravaca, preciznost i pravilnost u matematici, arhitekturi ili tehničkom crtanju jednostavno ne bi postojali. Oni koji žele razumjeti kako linije oblikuju svijet crta i ravnina ovdje mogu pronaći više od pukih definicija.
Osnovni pojmovi o pravcima

U matematici koristimo pojmove o pravcima za opisivanje položaja, odnosa i kutova između različitih geometrijskih elemenata. Bez toga, analitička geometrija, arhitektura i tehničko crtanje ne bi imali smisla.
Definicija pravca
Pravac je beskonačan niz točaka koje se protežu u jednom smjeru, bez početka i kraja. U geometriji ga opisujemo jednadžbom koja povezuje koordinate točaka u ravnini.
Na primjer, jednadžba y = kx + l prikazuje pravac s nagibom k i presjekom s osi y u točki l. U prostoru, određujemo pravac pomoću dviju različitih točaka kroz koje prolazi.
Pravac često predstavlja linearni odnos, smjer kretanja ili promjene. Za precizniji opis, koristimo parametarski oblik:
| Obilježje | Opis |
|---|---|
| Smjer | Određen vektorom |
| Položaj | Određen jednom poznatom točkom |
| Duljina | Beskonačna |
Važno je razlikovati pravac od dužine i polupravca. Dužina i polupravac imaju početak, ali ne traju beskonačno.
Vrste pravaca u ravnini
U ravnini razlikujemo tri osnovna odnosa: paralelni, okomiti i kosni pravci. Paralelni pravci imaju jednak nagib i ne sijeku se nikad.
Okomiti pravci sijeku se pod kutom od 90°, dok kosni tvore kut koji nije ni 0° ni 90°.
Primjer:
- Pravci y = 2x + 1 i y = 2x – 3 su paralelni jer im je nagib jednak (k₁ = k₂).
- Pravci y = 2x + 4 i y = -½x + 1 su okomiti jer vrijedi k₁ × k₂ = -1.
Ti odnosi pomažu nam da shvatimo orijentaciju likova u ravnini. U praksi ih koristimo u tehničkom crtanju, dizajnu zgrada ili čak u prometnim planovima.
Šiljasti kut i kut između pravaca
Kut između dvaju pravaca određujemo prema nagibu svakog od njih. Ako su nagibi k₁ i k₂, vrijedi formula:
[
tan(α) = left|frac{k_1 – k_2}{1 + k_1 k_2}right|
]
Kut može biti šiljasti (manji od 90°) ili tupi (veći od 90°). Kad su pravci okomiti, kut je točno 90°, a kad su paralelni, kut je 0°.
Šiljasti kut je važan u izračunima nagiba, smjera vektora i projekcijama. U crtežima i konstrukcijama, taj kut često koristimo za precizno usklađivanje elemenata.
Što su okomiti pravci
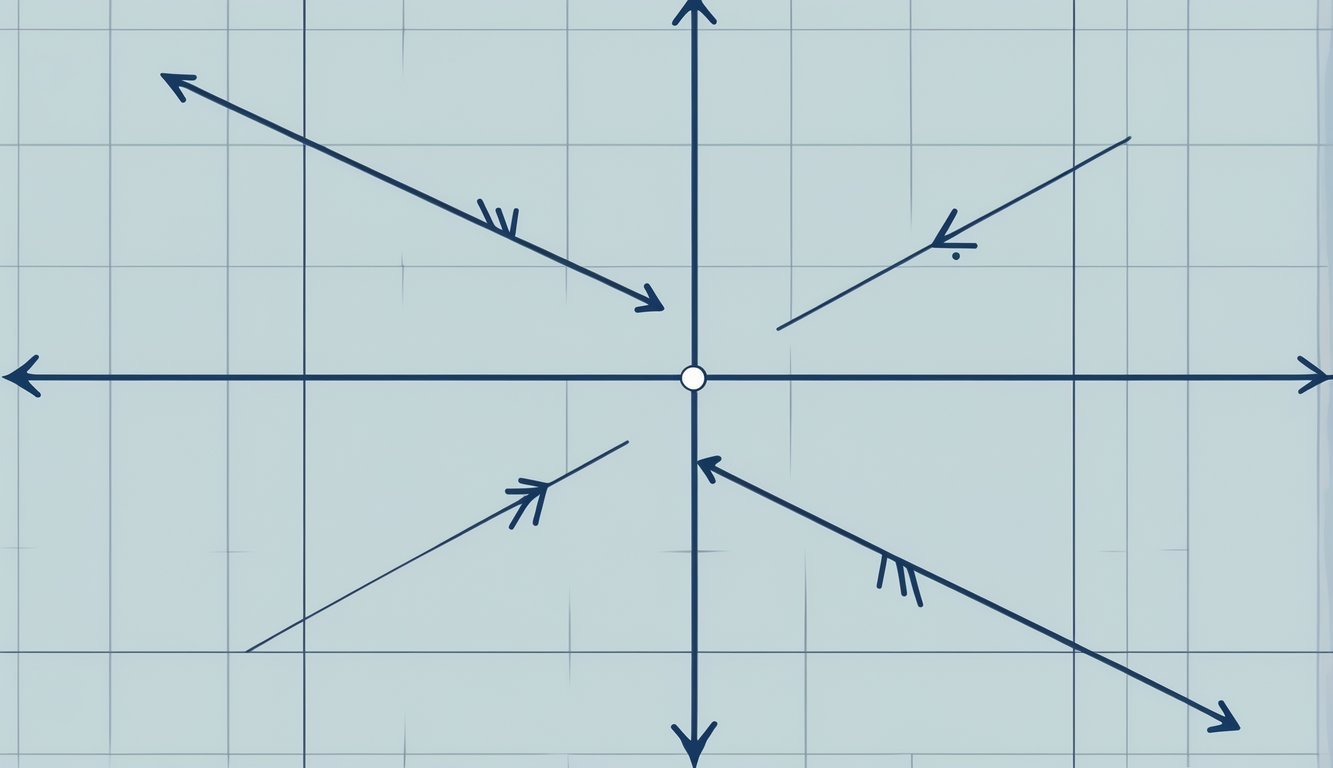
Okomiti pravci opisuju odnos dvaju pravaca koji se sijeku pod pravim kutom od 90°. Taj odnos igra ključnu ulogu u geometriji, arhitekturi i tehničkom crtanju jer jasno definira prostor i omogućuje stabilne konstrukcije.
Poznavanje okomitosti olakšava razumijevanje pojmova poput simetrale, koordinatnih osi i ravnina.
Značenje okomitosti u geometriji
U geometriji, okomitost znači da se dva pravca sijeku i tvore četiri jednaka kuta od po 90°. Takve pravce zovemo ortogonalnima.
Ako jedan pravac opisujemo jednadžbom (y = m_1x + b_1), a drugi (y = m_2x + b_2), uvjet okomitosti je (m_1 times m_2 = -1). Ovaj odnos olakšava prepoznavanje okomitih smjerova u koordinatnom sustavu.
Klasičan primjer su osi x i y u Kartezijevoj ravnini. One se sijeku u ishodištu (0,0) i čine osnovu za opisivanje svih točaka. U trodimenzionalnom prostoru, okomitost se širi na tri osi — x, y i z — koje zajedno određuju prostorni raspored.
Ovaj koncept koristimo u mjerenjima kutova, konstruiranju figura i određivanju nagiba površina. Bez okomitosti, ne bismo mogli pravilno primijeniti Pitagorin poučak ili konstruirati točne tlocrte.
Primjeri okomitih pravaca iz svakodnevnog života
Okomite pravce lako primijetimo oko sebe. Zidovi i podovi prostorija tvore okomite linije i tako daju zgradama stabilnost. Kad bi kut bio manji ili veći od 90°, zgrada bi bila klimava.
Građevinski majstori i arhitekti koriste libele da provjere okomitost dok grade. Na ulicama, mnogi gradovi imaju mrežu pravaca koji se sijeku pod pravim kutem – to olakšava orijentaciju i prometno planiranje.
U učionicama, rubovi ploče i okviri prozora su još jedan primjer okomitosti. U tehnici i dizajnu, okomiti smjerovi služe za izradu pravokutnih konstrukcija poput ormara, stolova i uređaja.
Čak i kod tehnologije, recimo kad postavljamo monitor na stol, održavanje pravog kuta poboljšava ergonomiju.
| Primjer | Opis upotrebe okomitosti |
|---|---|
| Zid i pod | Stabilnost zgrade i točan tlocrt |
| Ulice i avenije | Jasna orijentacija i prometna organizacija |
| Koordinatne osi | Matematičko definiranje položaja točaka |
| Tehnički crtež | Precizna konstrukcija oblika i kutova |
Matematički uvjet okomitosti pravaca
Okomitost pravaca u matematici opisuje točan odnos dvaju pravaca koji se sijeku pod pravim kutom. Taj odnos ne određujemo samo mjerenjem kuta, nego i primjenom određenih algebraičkih pravila koja proizlaze iz jednadžbe pravca.
Koeficijenti smjera i njihova povezanost
Koeficijent smjera (k) pokazuje nagib pravca prema osi x. Ukratko, govori nam koliko se y mijenja kad x naraste za jedan.
U ravnini, svaki pravac u obliku y = kx + l ima svoj koeficijent smjera. Taj broj određuje smjer i položaj pravca.
Kad se dva pravca sijeku, usporedba njihovih koeficijenata smjera otkriva njihov odnos. Ako su koeficijenti jednaki, pravci su paralelni.
Ako su koeficijenti suprotni recipročni brojevi, pravci su okomiti. Primjer: ako jedan pravac ima koeficijent k₁ = 2, drugi mora imati k₂ = -1/2 da bi bio okomit.
Ova veza olakšava analizu pravaca bez potrebe za mjerenjem kuteva. Iskreno, tko ima vremena za kutomjer?
Formula za uvjet okomitosti
Matematički izraz za okomite pravce u ravnini je:
k₁ · k₂ = -1
Taj uvjet vrijedi samo kad su pravci u eksplicitnom obliku y = kx + l. Ako su pravci zadani općim jednadžbama, kao što su A₁x + B₁y + C₁ = 0 i A₂x + B₂y + C₂ = 0, tada vrijedi:
A₁A₂ + B₁B₂ = 0
| Oblik pravca | Uvjet okomitosti |
|---|---|
| y = kx + l | k₁·k₂ = -1 |
| A₁x + B₁y + C₁ = 0 | A₁A₂ + B₁B₂ = 0 |
Oba izraza opisuju isti geometrijski odnos – kut između pravaca iznosi 90°. Prvi je češći u školskim zadacima jer je jednostavniji kad su pravci zadani nagibom.
Rješavanje zadataka s okomitim pravcima
U zadacima često treba pronaći jednadžbu pravca koji je okomit na zadani pravac i prolazi određenom točkom.
Prvo se pronađe koeficijent smjera zadanog pravca. Zatim iz uvjeta k₁·k₂ = -1 izračunamo novi koeficijent smjera.
Na primjer, ako zadani pravac ima jednadžbu y = 3x + 1, njegov okomiti pravac ima k = -1/3. Ako prolazi kroz točku A(0, 2), jednadžba je y = (-1/3)x + 2.
Takvi zadaci pomažu povezati algebru i geometriju u jedan postupak. Nekoliko provjera i malo algebre brzo otkriju jesu li pravci zaista okomiti.
Razlike između okomitih i paralelnih pravaca
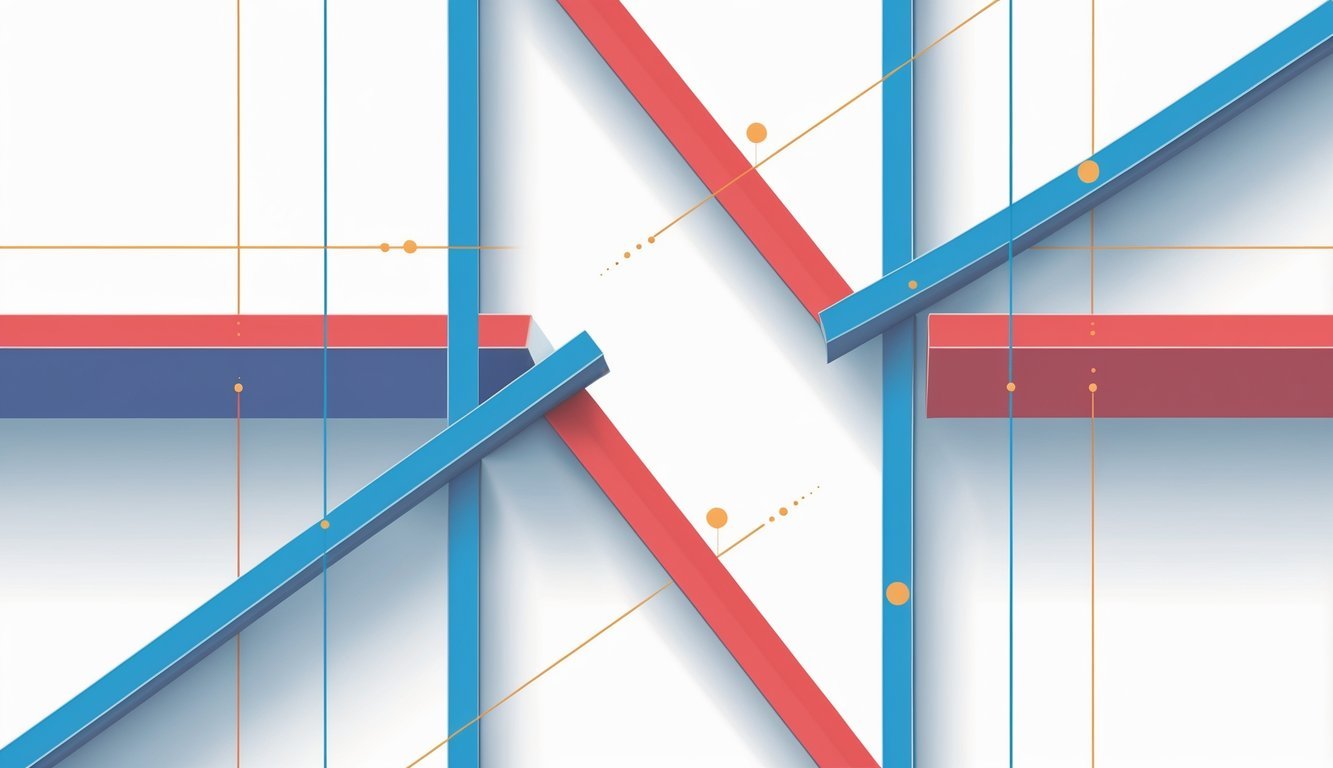
Okomiti i paralelni pravci određuju odnose u ravnini. Njihove razlike proizlaze iz načina na koji se sijeku i iz matematičkih uvjeta koji ih opisuju.
Matematičari često analiziraju te odnose kroz jednadžbe pravaca. Nije loše imati takav alat pri ruci.
Uvjet paralelnosti
Dva pravca su paralelna ako se nikada ne sijeku. To znači da imaju isti koeficijent smjera.
U jednadžbi pravca to znači
[
k_1 = k_2
]
kad su zapisani kao y = kx + l.
Ako koristimo opće oblike jednadžbi, paralelnost vrijedi kad postoji omjer:
[
frac{A_1}{A_2} = frac{B_1}{B_2}
]
Paralelni pravci zadržavaju jednak razmak cijelom dužinom. Zidovi zgrade ili tračnice željeznice su dobar primjer.
Za razliku od njih, okomiti pravci sijeku se pod kutom od 90°. Taj odnos opisuje uvjet:
[
k_1 cdot k_2 = -1
]
što znači da je nagib jednog pravca negativni recipročan nagibu drugog.
U ovoj tablici nalazi se kratki pregled:
| Vrsta pravaca | Uvjet smjera | Geometrijski odnos |
|---|---|---|
| Paralelni | ( k_1 = k_2 ) | Ne sijeku se |
| Okomiti | ( k_1 cdot k_2 = -1 ) | Sijeku se pod kutom od 90° |
Analiza paralelnih i okomitih pravaca kroz primjere
Ako uzmemo pravac y = 2x + 1, paralelan pravac ima isti nagib, recimo y = 2x – 3.
Bez obzira na slobodni član, linije se nikada ne susreću. S druge strane, pravac koji je okomit na njega ima nagib –1/2.
Na primjer, y = –½x + 4 siječe prvi pravac pod pravim kutom.
Graditelji koriste okomite pravce za stabilnost. Zid i pod moraju biti okomiti da bi konstrukcija bila ispravna.
Paralelni pravci pak donose simetriju i ravnotežu, kao u arhitekturi ili prometnim trakama. Razlikovanje ovih odnosa ključno je u geometriji jer svaka promjena nagiba mijenja kut između pravaca.
Primjene okomitih pravaca u matematici

Okomiti pravci igraju važnu ulogu u analitičkoj geometriji i konstrukciji likova. Oni omogućuju točna mjerenja, određivanje kutova i pravilno oblikovanje geometrijskih figura u ravnini i prostoru.
Poznavanje njihovih odnosa temelj je za razumijevanje mnogih matematičkih pojmova. Ne može se baš bez toga.
Okomiti pravci u crtama i grafovima
U matematici su okomiti pravci ključni za prikaz odnosa funkcija i analizu nagiba. Dva pravca su okomita ako se sijeku pod kutom od 90°, odnosno ako umnožak njihovih koeficijenata smjera iznosi –1.
Primjerice, ako je jedan pravac y = 2x + 3, okomit na njega ima smjer –1/2.
Takav odnos koristi se u prikazu linearnih grafova, konstrukciji normala na krivulje i određivanju tangentnih pravaca. U koordinatnom sustavu, okomiti pravci pomažu pri određivanju udaljenosti između točaka.
Tablica prikazuje osnovni odnos:
| Vrsta odnosa pravaca | Matematički uvjet | Geometrijsko značenje |
|---|---|---|
| Paralelni pravci | a₁ = a₂ | Pravci se ne sijeku |
| Okomiti pravci | a₁ · a₂ = –1 | Pravci se sijeku pod 90° |
Ova pravila olakšavaju analizu grafova linearnih funkcija i pomažu razumjeti njihove odnose. To je temeljna vještina za geometrijsko modeliranje, htjeli mi to ili ne.
Uloga u konstrukciji geometrijskih likova
U konstrukciji likova, okomiti pravci pomažu kod izrade preciznih dijelova figura poput kvadrata, pravokutnika i trokuta s pravim kutom. Ljudi u praksi često posegnu za šestarom ili trokutnjakom da povuku linije koje tvore pravi kut.
U geometrijskim zadacima, crtam okomiti pravac kroz određenu točku i na zadani pravac. Na taj način mogu lako dobiti visine u trokutu ili normale na stranice mnogokuta.
Ovi pravci igraju ključnu ulogu kod određivanja projekcija i udaljenosti između točke i pravca u prostoru. Bez okomitosti, teško bih mogao jasno definirati pojmove poput visine tijela ili normalnog presjeka.
Njihova primjena širi se i na nacrtnu geometriju. Tamo omogućuju prikaz trodimenzionalnih oblika na ravnoj plohi, što je zapravo fascinantno kad malo bolje razmislim.