Kružnica nije samo oblik koji se često crta na papiru, već i važan dio matematike koji pomaže razumjeti odnose u koordinatnom sustavu. Jednadžba kružnice opisuje skup svih točaka u ravnini koje su jednako udaljene od središta. To znači da se svaka kružnica može zapisati preciznom matematičkom formulom.
Ono što u početku izgleda kao suha teorija zapravo otvara vrata razumijevanju mnogih zadataka – od određivanja udaljenosti između točaka, do proučavanja odnosa kružnice i pravca. Kada se jednom shvati logika iza standardnog i općeg oblika jednadžbe, sve ostalo postaje puno jasnije.
Tko želi vidjeti kako se kružnica ponaša u različitim položajima ili kako dvije kružnice mogu dijeliti zajedničke točke, brzo će shvatiti da se iza jednostavne formule krije cijeli svijet zanimljivih primjena.
Osnovni pojmovi kružnice

Kružnica u matematici označava skup svih točaka u ravnini koje su jednako udaljene od jedne stalne točke. Ta stalna točka zove se središte, a udaljenost od središta do bilo koje točke na kružnici naziva se radijus ili polumjer.
Jednostavno rečeno, ako netko uzme šestar, zabode ga u papir i povuče luk, ono što dobije jest kružnica. Središte je mjesto gdje se šestar zabio, a radijus je dužina između tog mjesta i olovke.
Za bolje pamćenje, korisno je razlikovati pojmove:
| Pojam | Objašnjenje |
|---|---|
| Kružnica | Skup točaka jednako udaljenih od središta |
| Krug | Površina omeđena kružnicom |
| Radijus | Udaljenost središta do bilo koje točke na kružnici |
U praksi, radijus se često koristi u svakodnevnim mjerenjima. Primjerice, kod kotača bicikla radijus određuje veličinu kotača, a time i koliko se brzo vozi pri istoj brzini okretanja pedala.
Kružnica se u matematici ne koristi samo za crtanje. Ona je temelj za jednadžbu kružnice koja opisuje sve točke tog skupa pomoću koordinata. To omogućuje rješavanje zadataka u geometriji, fizici i tehnici.
Učenici se najčešće prvi put susreću s ovim pojmovima u osnovnoj školi, a kasnije ih proširuju kroz algebru i analitičku geometriju. Tako se kružnica pretvara iz jednostavnog crteža u precizan matematički objekt.
Standardni oblik jednadžbe kružnice

Standardni oblik jednadžbe kružnice omogućuje jednostavno prepoznavanje središta i radijusa. Ovaj zapis izdvaja bitne parametre pa se odmah vidi gdje se kružnica nalazi i kolika joj je veličina.
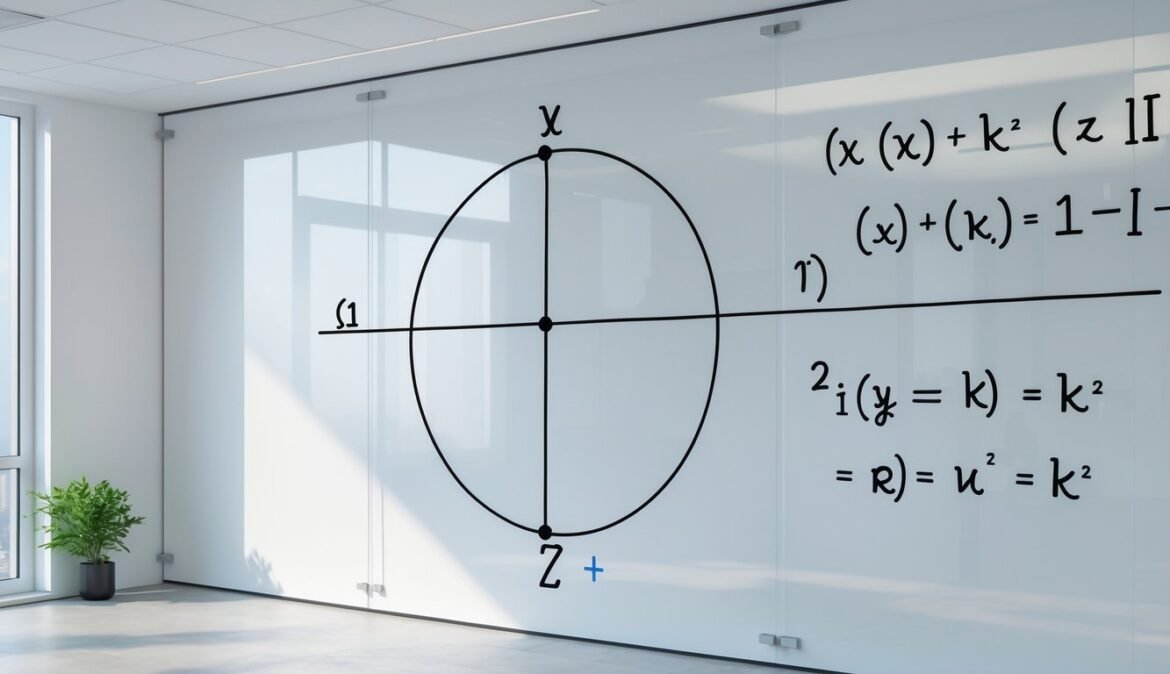
Jednadžba sa središtem u ishodištu
Kada je središte kružnice u ishodištu koordinatnog sustava, jednadžba poprima vrlo jednostavan oblik:
[ x^2 + y^2 = r^2 ]
Ovdje je (r) radijus kružnice. Svi parovi ((x, y)) koji zadovoljavaju ovu jednadžbu nalaze se točno na kružnici.
Primjer: ako je radijus (r = 5), jednadžba glasi (x^2 + y^2 = 25). To znači da je svaka točka udaljena 5 jedinica od ishodišta.
Ovaj oblik se često koristi u zadacima jer je pregledan i lako se uočava simetrija kružnice oko ishodišta.
Jednadžba sa središtem u točki (p, q)
Ako se središte ne nalazi u ishodištu, jednadžba se malo mijenja:
[ (x – p)^2 + (y – q)^2 = r^2 ]
Točka ((p, q)) označava središte, a (r) je radijus. Ovim zapisom kružnica se može smjestiti bilo gdje u ravnini.
Primjer: neka je središte u ((3, -2)), a radijus (4). Jednadžba tada glasi ((x – 3)^2 + (y + 2)^2 = 16). Svaka točka koja zadovoljava ovaj uvjet leži na kružnici udaljenoj 4 jedinice od točke ((3, -2)).
Ovaj oblik je posebno važan u geometrijskim zadacima jer omogućuje precizno određivanje položaja kružnice.
Tumačenje parametara
U standardnom obliku jasno se vide ključni elementi:
- Središte kružnice: određeno s ((p, q))
- Radijus: jednak je (\sqrt{r^2} = r)
- Jednadžba: opisuje skup svih točaka jednako udaljenih od središta
Ako je (r = 0), kružnica se svodi na jednu točku ((p, q)). Ako je (r) negativan, jednadžba nema smisleno rješenje jer radijus ne može biti manji od nule.
Na ovaj način jednadžba ne samo da opisuje kružnicu, nego i otkriva sve što je potrebno za crtanje ili daljnje računanje.
Opći oblik jednadžbe kružnice

Opći oblik jednadžbe kružnice zapisuje se kao:
x² + y² + Dx + Ey + F = 0
Ovaj oblik izgleda jednostavno, ali na prvi pogled ne otkriva odmah središte ni polumjer kružnice. Za to je potrebno napraviti svođenje na potpuni kvadrat.
Primjerice, kada se članovi grupiraju i nadopune do kvadrata, jednadžba prelazi u tzv. standardni oblik:
(x – a)² + (y – b)² = r².
Tada se jasno vide koordinate središta kružnice (a, b) i njezin polumjer r.
Važno je znati da opći oblik ne mora uvijek predstavljati kružnicu. Ako se nakon sređivanja dobije negativna vrijednost za r², tada u ravnini zapravo nema kružnice. Ako je r = 0, jednadžba opisuje samo jednu točku.
Za brži pregled, evo male usporedbe:
| Oblik jednadžbe | Primjer | Što pokazuje odmah |
|---|---|---|
| Opći oblik | x² + y² + 4x – 6y + 9 = 0 | Ne vidi se središte ni polumjer |
| Standardni oblik | (x + 2)² + (y – 3)² = 4 | Središte (–2, 3), polumjer 2 |
U školskim zadacima često se traži upravo pretvaranje iz općeg u standardni oblik. Na taj način učenici uče kako iz jednadžbe „izvući“ geometrijski smisao i prepoznati kružnicu u ravnini.
Posebni slučajevi i položaji kružnice
Kružnica u koordinatnom sustavu može zauzeti nekoliko zanimljivih položaja. Neki od njih olakšavaju računanje jer se jednadžba kružnice jednostavno zapisuje.
Primjer je središnja kružnica sa središtem u ishodištu koordinatnog sustava. Njezina jednadžba poprima oblik:
x² + y² = r²
Ovdje se lako očita polumjer, a računanje udaljenosti postaje jednostavnije nego kod pomaknutih kružnica.
Postoje i koncentrične kružnice – više kružnica koje dijele isto središte, ali imaju različite polumjere. Takva situacija često se koristi u zadacima gdje se uspoređuju udaljenosti ili površine.
Zanimljivi su i položaji kada kružnica dodiruje koordinatne osi. Ako kružnica dodiruje samo jednu os, tada je polumjer jednak udaljenosti središta od te osi. Ako dodiruje obje osi, središte se nalazi jednako udaljeno od njih, što znači da su koordinate središta jednake veličine.
Za brzi pregled:
| Položaj kružnice | Posebnost u jednadžbi |
|---|---|
| Središte u ishodištu | x² + y² = r² |
| Koncentrične kružnice | isto središte, razni r |
| Dodiruje jednu koordinatnu os | r = udaljenost od osi |
| Dodiruje obje osi | koordinate središta jednake |
Ovi posebni slučajevi pokazuju kako se jednadžba kružnice može pojednostaviti ili brzo prepoznati u zadacima.
Međusobni odnosi kružnice i pravca
Kružnica i pravac u ravnini mogu imati različite odnose, a sve ovisi o tome koliko zajedničkih točaka dijele. Jednostavno rečeno, pravac može presjeći kružnicu, dodirnuti je ili je potpuno mimoići.
Za razumijevanje ovih odnosa koristi se jednadžba kružnice i jednadžba pravca. Kada se linearna jednadžba pravca uvrsti u jednadžbu kružnice, dobiva se kvadratna jednadžba. Njezina diskriminanta određuje konačan odnos.
Najčešće se razlikuju tri slučaja:
- Sekanta – pravac siječe kružnicu u dvije točke.
- Tangenta – pravac dodiruje kružnicu u jednoj točki.
- Mimoilaženje – pravac i kružnica nemaju zajedničkih točaka.
Za lakši pregled:
| Odnos | Broj zajedničkih točaka | Naziv pravca |
|---|---|---|
| Presjek | 2 | Sekanta |
| Dodir | 1 | Tangenta |
| Nema sjecišta | 0 | Mimoilaze se |
Primjer iz prakse: učenici često crtaju kružnicu i pravac na koordinatnoj mreži pa rješavaju sustav jednadžbi. Ako dobiju dva rješenja, to su koordinate presjeka. Ako je rješenje samo jedno, to je točka dodira. A ako nema stvarnih rješenja, pravac i kružnica se jednostavno ne susreću.
Ovaj pristup povezuje geometriju i algebru jer pokazuje kako se vizualni odnosi mogu izračunati pomoću jednadžbi.
Položaj i odnosi dviju kružnica
Kad se promatraju dvije kružnice u ravnini, njihov međusobni položaj ovisi o udaljenosti između središta i duljini polumjera. Jednadžbe kružnice pomažu jasno opisati te odnose.
Postoji nekoliko osnovnih situacija:
- Nemaju zajedničkih točaka – kružnice su udaljene ili se jedna nalazi unutar druge bez dodira.
- Dodiruju se izvana – imaju jednu zajedničku točku, a središta su udaljena za zbroj polumjera.
- Dodiruju se iznutra – također imaju jednu točku dodira, ali je udaljenost središta jednaka razlici polumjera.
- Sijeku se – imaju dvije zajedničke točke.
- Podudarne su – imaju isto središte i isti polumjer.
Za brži pregled:
| Položaj kružnica | Broj zajedničkih točaka | Uvjet (udaljenost središta d) |
|---|---|---|
| Razdvojene | 0 | d > r₁ + r₂ |
| Jedna unutar druge (bez dodira) | 0 | d < |
| Vanjski dodir | 1 | d = r₁ + r₂ |
| Unutarnji dodir | 1 | d = |
| Sijeku se | 2 | |
| Podudarne | beskonačno | d = 0 i r₁ = r₂ |
Jednadžbe kružnice u koordinatnom sustavu omogućuju provjeru ovih uvjeta. Računanje udaljenosti između središta i usporedba s polumjerima daje točan odgovor o tome u kojem se odnosu dvije kružnice nalaze.
Ovakav pristup olakšava rješavanje zadataka iz geometrije, ali i vizualizaciju položaja kružnica na crtežu.