Na prvi pogled, Gaussova ravnina izgleda kao još jedan koordinatni sustav iz matematike. Ipak, ona otkriva nešto više — način na koji možemo apstraktne kompleksne brojeve prikazati u stvarnom, vizualnom prostoru.
Ovaj pristup pomaže nam razumjeti odnose između realnih i imaginarnih dijelova broja na puno intuitivniji način.
Gaussova ravnina je dvodimenzionalni sustav u kojem kompleksne brojeve prikazujemo kao točke, pri čemu realni dio ide vodoravno, a imaginarni okomito.
Kako iz jednog broja izvući duljinu, kut ili simetriju? Kroz Gaussovu ravninu geometrija se isprepliće s algebrom, pa pojmovi poput modula, argumenta ili konjugiranih brojeva zapravo postaju mnogo jasniji.
Ako želiš svladati osnove — od algebarskog prikaza do geometrijske interpretacije — ovdje ćeš naći put kroz ovu temu.
Osnove kompleksnih brojeva
Kompleksni brojevi povezuju realne i imaginarne veličine u jedan sustav. Oni nam omogućuju rješavanje jednadžbi koje nemaju rješenja u skupu realnih brojeva i daju geometrijsku sliku kroz prikaz u Gaussovoj ravnini.
Definicija kompleksnog broja
Kompleksni broj zapisujemo kao z = x + yi, gdje su x i y realni brojevi, a i označava imaginarni dio. Ovaj zapis spaja dva broja u jedan izraz koji ne možemo prikazati samo na realnoj osi.
Skup kompleksnih brojeva označavamo slovom ℂ, a svaka točka u tom skupu odgovara uređenom paru (x, y) u ravnini. Tako svaki kompleksni broj ima aritmetičko i geometrijsko značenje.
Zbrajanje i oduzimanje kompleksnih brojeva svodi se na zbrajanje realnih i imaginarnih dijelova posebno. Na primjer:
- (2 + 3i) + (1 + 4i) = 3 + 7i
Kod množenja koristimo pravilo i² = −1, što kompleksnim brojevima daje posebna svojstva.
Imaginarna jedinica i imaginarni brojevi
Imaginarna jedinica je označena slovom i i zadovoljava jednadžbu i² = −1. Ona je polazna točka za sve imaginarne i kompleksne brojeve.
Svaki imaginarni broj ima oblik yi, gdje je y realan broj. Kad je y = 0, broj je realan; kad je x = 0, broj je čisto imaginaran.
Imaginarna jedinica ima zanimljiv niz potencija koji se ponavlja svakih četiri koraka:
| Potencija | Vrijednost |
|---|---|
| i¹ | i |
| i² | −1 |
| i³ | −i |
| i⁴ | 1 |
Ovaj periodičan uzorak često koristimo kad pojednostavljujemo izraze s imaginarnim jedinicama.
Realni i imaginarni dio kompleksnog broja
U izrazu z = x + yi, realni dio označavamo kao Re(z) = x, a imaginarni dio kao Im(z) = y. Oba su realni brojevi, ali svaki ima svoju ulogu u prikazu točke u kompleksnoj ravnini.
Realni dio leži na realnoj osi (x‑osi), dok imaginarni dio određuje položaj na imaginarnoj osi (y‑osi). Skupa, oni čine točku (x, y) u ravnini, gdje je udaljenost od ishodišta dana formulom |z| = √(x² + y²).
Ovaj prikaz omogućuje geometrijsku interpretaciju računskih operacija. Zbrajanje kompleksnih brojeva možemo shvatiti kao pomak točaka u ravnini, dok modul pokazuje udaljenost od ishodišta — neku vrstu „veličine” kompleksnog broja.
Algebarski prikaz i računske operacije
U Gaussovoj ravnini svaki kompleksni broj ima jasnu strukturu. Svaki broj prikazujemo pomoću realnog i imaginarnog dijela.
Taj oblik omogućuje jednostavno izvođenje osnovnih računskih operacija i lakše razumijevanje njihove geometrijske strane.
Algebarski oblik kompleksnog broja
Algebarski prikaz kompleksnog broja izgleda kao z = x + yi, gdje su x i y realni brojevi, a i je imaginarna jedinica (i² = –1). Dio x nazivamo realnim dijelom (Re z), a y imaginarnim dijelom (Im z).
U Gaussovoj ravnini svaka točka ((x, y)) odgovara kompleksnom broju. Osa x predstavlja realne brojeve, a osa y imaginarne.
Kompleksni broj u ravnini možemo zamisliti kao vektor iz ishodišta ((0,0)) do točke ((x, y)).
| Dijelovi kompleksnog broja | Oznaka | Značenje |
|---|---|---|
| Realni dio | Re z | Koordinata na realnoj osi |
| Imaginarni dio | Im z | Koordinata na imaginarnoj osi |
| Modul | |z| = √(x² + y²) | Udaljenost točke od ishodišta |
| Argument | φ = arctan(y/x) | Kut vektora s realnom osi |
Ovakav prikaz čini algebarske operacije – zbrajanje, oduzimanje, množenje i dijeljenje – preglednima i matematički dosljednima.
Zbrajanje i oduzimanje
Kod zbrajanja i oduzimanja kompleksnih brojeva zbrajamo ili oduzimamo odgovarajuće dijelove. Ako imamo
(z₁ = x₁ + y₁i) i (z₂ = x₂ + y₂i), tada:
[
z₁ + z₂ = (x₁ + x₂) + (y₁ + y₂)i
]
[
z₁ – z₂ = (x₁ – x₂) + (y₁ – y₂)i
]
Na Gaussovoj ravnini ove operacije imaju jasnu geometrijsku interpretaciju: zbrajanje odgovara sabrajanju vektora, a oduzimanje oduzimanju vektora.
Rezultat zbrajanja zapravo je dijagonala paralelograma kojeg formiraju vektori (z₁) i (z₂).
Primjer:
Ako (z₁ = 2 + 3i) i (z₂ = 1 – 2i), onda je
(z₁ + z₂ = 3 + i), a (z₁ – z₂ = 1 + 5i).
Realni i imaginarni dijelovi u operacijama ostaju potpuno odvojeni.
Množenje i dijeljenje kompleksnih brojeva
Za množenje koristimo distributivnost i pravilo i² = –1.
Ako su (z₁ = x₁ + y₁i) i (z₂ = x₂ + y₂i), tada:
[
z₁ times z₂ = (x₁x₂ – y₁y₂) + (x₁y₂ + x₂y₁)i
]
Ova formula pokazuje kako se realni i imaginarni dijelovi međusobno kombiniraju. Množenjem zapravo „rotiramo” i mijenjamo duljinu vektora u ravnini, što postaje korisno kad prijeđemo na trigonometrijski oblik.
Dijeljenje radimo pomoću konjugiranog broja. Kompleksni broj (z = x + yi) ima konjugirani oblik (z̅ = x – yi).
Za dvije vrijednosti (z₁) i (z₂) vrijedi:
[
frac{z₁}{z₂} = frac{z₁ cdot z̅₂}{x₂^2 + y₂^2}
]
Taj postupak uklanja imaginarni dio iz nazivnika.
Primjer:
[
frac{1 + i}{1 – i} = frac{(1 + i)(1 + i)}{(1 – i)(1 + i)} = frac{2i}{2} = i
]
Na taj način i složenije operacije s kompleksnim brojevima postaju jasnije i preciznije.
Gaussova ravnina i kompleksna ravnina
Gaussova ravnina pomaže nam da lakše shvatimo kompleksne brojeve. Na toj ravnini stvarni i imaginarni dijelovi postaju jasni, a njihova veza olakšava izračune i tumačenje matematičkih odnosa.
Definicija Gaussove ravnine
Gaussova ravnina, ili kompleksna ravnina, je dvodimenzijski sustav za prikaz kompleksnih brojeva. Svaki broj u obliku z = a + bi postaje točka u toj ravnini.
Vrijednost a je realni dio, dok b označava imaginarni dio broja. Ravnina zapravo izgleda kao običan kartezijanski sustav.
Na horizontalnoj osi nalazimo realne brojeve, a na vertikalnoj imaginarne. Ovakav prikaz omogućuje da pojmove poput zbrajanja i oduzimanja prikažemo grafički.
Carl Friedrich Gauss uveo je ovaj koncept. On je povezao algebru i geometriju, pa je kompleksni broj dobio i prostorni smisao.
Prikaz brojeva na Gaussovoj ravnini
Svaki kompleksni broj ima položaj određen koordinatama (a, b). Na primjer, broj z = 3 + 2i leži tri jedinice desno od ishodišta i dvije jedinice prema gore.
Takav prikaz omogućuje jednostavno uspoređivanje i nalaženje odnosa među brojevima. U geometriji koristimo pojam modula kompleksnog broja – on pokazuje udaljenost točke od ishodišta i računa se preko izraza √(a² + b²).
Bitan je i argument, kut između realne osi i dužine koja spaja ishodište s točkom. Zbrajanje i oduzimanje kompleksnih brojeva možemo prikazati konstrukcijom trokuta ili paralelograma.
Uloga realne i imaginarne osi
U Gaussovoj ravnini realna os prikazuje sve realne brojeve. Leži vodoravno i određuje smjer stvarnih dijelova.
Imaginarna os okomita je na realnu i prikazuje imaginarne dijelove, nastale množenjem s jedinicom i koja zadovoljava i² = –1. Ta podjela pomaže matematičarima i fizičarima da analiziraju kompleksne odnose, primjerice fazne pomake u električnim krugovima ili talasne funkcije u kvantnoj mehanici.
Točka na realnoj osi prikazuje broj bez imaginarnog dijela, dok čista imaginarna vrijednost leži na vertikalnoj osi. Svaka kombinacija realnog i imaginarnog dijela ima točno mjesto u ravnini, pa postaje puno lakše vizualizirati kompleksne veličine.
Modul i geometrijska interpretacija
U Gaussovoj ravnini svaki kompleksni broj ima svoju udaljenost od ishodišta i položaj koji pokazuje njegov stvarni i imaginarni dio. Modul i način prikaza brojeva u koordinatnom sustavu temelj su za razumijevanje odnosa među kompleksnim brojevima.
Modul kompleksnog broja
Modul kompleksnog broja označava duljinu vektora koji prikazuje taj broj u Gaussovoj ravnini. Ako kompleksni broj pišemo kao z = a + bi, njegov modul izračunavamo ovako:
[
|z| = sqrt{a^2 + b^2}
]
Ta vrijednost je uvijek nenegativna i pokazuje udaljenost točke (a, b) od ishodišta. Drugim riječima, modul nam govori koliko je broj “velik”, bez obzira na smjer.
Kod realnih brojeva, modul ima sličnu ulogu kao apsolutna vrijednost. Na primjer, brojevi 3 + 4i i −3 − 4i imaju isti modul jer su jednako udaljeni od ishodišta.
Taj koncept olakšava uspoređivanje vrijednosti i pisanje brojeva u trigonometrijskom obliku.
Udaljenost kompleksnih brojeva
Udaljenost između dva kompleksna broja računamo kao udaljenost između dviju točaka u ravnini. Ako imamo z₁ = a₁ + b₁i i z₂ = a₂ + b₂i, udaljenost je:
[
d = |z₁ – z₂| = sqrt{(a₁ – a₂)^2 + (b₁ – b₂)^2}
]
Ova mjera pomaže nam usporediti položaje brojeva bez crtanja grafa. Recimo, z₁ = 2 + i i z₂ = 5 + 3i – njihova udaljenost je (sqrt{(3)^2 + (2)^2} = sqrt{13}).
Udaljenost često koristimo kod zadataka s kružnicama, pravcima ili jednakim modulima. Tako povezujemo kompleksne brojeve s pojmovima iz analitičke geometrije.
Geometrijska interpretacija brojeva
Kompleksne brojeve prikazujemo u Gaussovoj ravnini tako da realni dio bude na horizontalnoj osi, a imaginarni na vertikalnoj. Svaki broj odgovara jednoj točki ili, preciznije, jednom vektoru iz ishodišta.
Kut između realne osi i vektora zovemo argument kompleksnog broja. On pokazuje smjer broja, dok modul pokazuje duljinu.
U trigonometrijskom obliku zapisujemo broj ovako:
[
z = |z|(cos varphi + isin varphi)
]
Ovaj prikaz zapravo olakšava množenje i dijeljenje kompleksnih brojeva. Geometrijski prikaz nije samo ilustracija, već alat koji povezuje algebru i geometriju u jedan sustav.
Konjugirano kompleksni brojevi
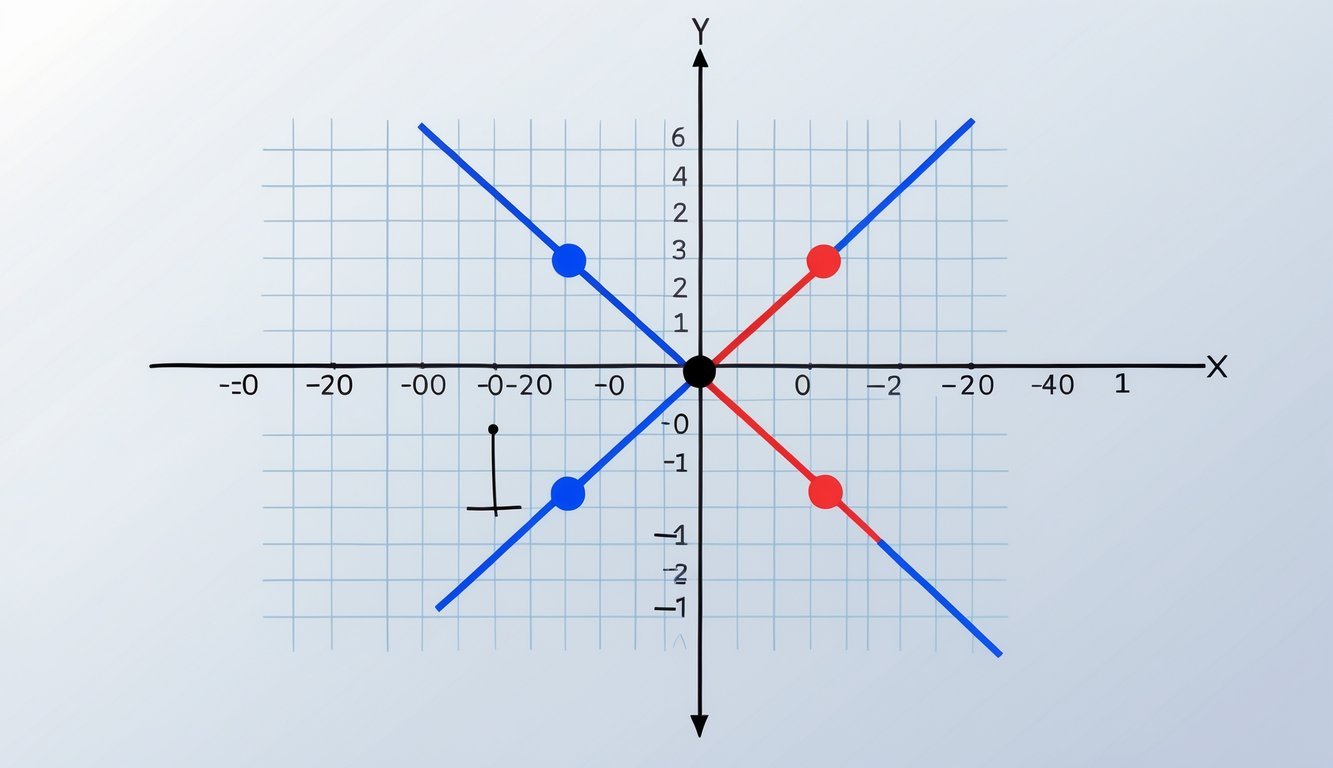
Svojstva konjugiranih kompleksnih brojeva pomažu nam da lakše računamo i shvatimo odnose u Gaussovoj ravnini. Njihova veza s realnom osi i geometrijska simetrija čine ih posebno zanimljivima za vizualni prikaz.
Definicija konjugiranog kompleksnog broja
Svaki kompleksni broj ima oblik z = x + iy, gdje je x realni, a y imaginarni dio. Njegov konjugirani broj zapisujemo kao z̄ = x − iy.
Konjugiranje mijenja predznak imaginarnog dijela, dok realni dio ostaje isti. Ta jednostavna operacija ima veliku važnost u matematici.
Konjugirani brojevi često pomažu kod dijeljenja kompleksnih brojeva, jer omogućuju uklanjanje imaginarne jedinice iz nazivnika. Kad broj z₁ dijelimo s z₂, lakše dobijemo rezultat ako množimo brojilac i nazivnik s z̄₂.
Tako dobijemo realniji prikaz izraza, a računanje modula ili argumenata postaje jednostavnije.
| Pojam | Značenje |
|---|---|
| z = x + iy | Kompleksni broj |
| z̄ = x − iy | Konjugirani kompleksni broj |
| x, y ∈ ℝ | Realni i imaginarni dio broja |
Kad množimo broj i njegov konjugat, uvijek dobijemo realan rezultat: z · z̄ = x² + y². To je korisno, primjerice, kod računanja modula kompleksnog broja.
Simetrija u Gaussovoj ravnini
U Gaussovoj ravnini, svaka točka prikazuje jedan kompleksni broj. Kad prikažemo broj z = x + iy kao točku ((x, y)), njegov konjugat z̄ = x − iy sjedi na ((x, -y)).
Te dvije točke leže simetrično u odnosu na realnu os. Realna os zapravo djeluje kao zrcalo—preslikava brojeve iz gornje u donju poluravninu i obratno.
Ova simetrija čini odnose među kompleksnim brojevima puno lakšima za prepoznati. Na primjer, broj u prvom kvadrantu ima svoj konjugat u četvrtom.
Takav prikaz pomaže kad pokušavamo shvatiti pojmove poput modula i argumenta. Konjugirani brojevi uvijek imaju jednak modul, ali suprotan argument.
Ne mogu reći da je Gaussova ravnina samo apstrakcija. Ljudi je stalno koriste za analizu električnih krugova, valova ili rotacija u prostoru.
Kompleksni brojevi, kroz ovu ravninu, postaju alat za opisivanje dvodimenzijskih pojava. Sve to čini Gaussovu ravninu korisnim modelom u tehničkim i prirodnim znanostima.